Cryptology is the arithmetic, comparable to quantity idea and the appliance of formulation and algorithms, that underpin cryptography and cryptanalysis. Cryptanalysis ideas are extremely specialised and sophisticated, so this definition concentrates on a few of the key mathematical ideas behind cryptography, in addition to fashionable examples of its use.
Fundamentals of cryptology
The phrases cryptology and cryptography are sometimes confused or used synonymously, however they aren’t the identical. Cryptology is a broad space that features cryptography and cryptanalysis. It’s derived from two Greek phrases: kryptós which means hidden and lógos which means phrase.
Cryptography is about creating guidelines and rules — algorithms, protocols and so forth — which are then used to safe information from unauthorized or malicious entry. Cryptanalysis is about utilizing strategies to interrupt cryptographic safety techniques with the intention to get better encrypted messages with out understanding the decryption key. Since cryptology incorporates ideas of each cryptography and cryptanalysis, it’s a superset of these applied sciences.
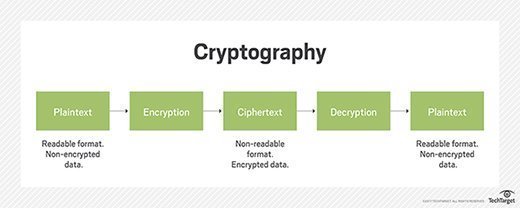
Cryptology is concerning the scientific research of safe communications and utilizing mathematical equations, frameworks and calculations to create robust safety techniques that may retailer information in safe, encrypted (secret) kind. For information to be secured for storage or transmission, it have to be reworked in such a way that it’s troublesome for an unauthorized particular person to find its true which means. To attain that, safety techniques and software program use sure mathematical equations which are troublesome to resolve except strict standards are met. The extent of issue of fixing a given equation is called its intractability. The equations kind the idea of cryptography.
Forms of cryptology equations
A number of the most vital equations utilized in cryptology are the next.
Discrete logarithm downside
The discrete logarithm downside (DLP) is without doubt one of the cornerstones of the fields of cryptology and cryptography. It’s described utilizing a finite cyclic group G with a generator g (primitive root modulo p); a component h, the place h is a component within the group G and generated by g; and a chief quantity P, a quantity that’s solely divisible by 1 and by itself, and it’s involved with discovering an integer x to fulfill the next method:
gx = h (mod P)
Merely put, the aim of DLP is to find out the exponent x given a base g, a outcome h and the modulo P.
One of the best ways to explain DLP is first to point out how its inverse idea works. Assume there’s a prime quantity P that could be a massive prime variety of over 300 digits, plus two different integers, a and b. Now, to seek out the worth of N, use the next method:
N = ab mod P, the place 0 ≤ N ≤ (P · 1)
This is called discrete exponentiation and is kind of easy to compute. Nonetheless, the other is true when inverted. Given P, a and N and a requirement to seek out b in order that the equation is legitimate, then there’s a super degree of issue. This downside varieties the idea for quite a few public key infrastructure (PKI) algorithms, comparable to Diffie-Hellman and ElGamal, which is why DLP is taken into account vital in cryptology.
Integer factorization downside
The integer factorization downside is worried with discovering the prime elements of a giant composite quantity. For instance, take two prime numbers, P2 and P1, that are each massive — a relative time period, the definition of which continues to maneuver ahead as computing energy will increase. Multiply these two primes to supply the product, N.
Thus, the easy method for the issue is the next:
P1 · P2 = N
The problem arises in, given N, looking for the unique P1 and P2.
To simplify issues to a fantastic diploma, the N product is the public key, and the P1 and P2 numbers are, collectively, the personal key.
The Rivest-Shamir-Adleman (RSA) PKI encryption protocol is without doubt one of the many algorithms based mostly on this downside.
The issue is vital for RSA and for different cryptosystems due to the next:
- It assumes that factoring massive numbers is computationally infeasible.
- If it may be proven that somebody can carry out the factoring effectively, then it may be demonstrated that RSA encryption is insecure.
Different cryptographic algorithms additionally use the integer factorization downside. Examples embrace Pollard’s rho algorithm, a special-purpose factorization algorithm and Dixon’s factorization methodology, which is a general-purpose integer factorization algorithm.
Elliptic-curve discrete logarithm downside
The elliptic-curve DLP (ECDLP) is a cryptographic protocol based mostly upon a fairly well-known mathematical downside. It’s involved with reversing scalar multiplication on an elliptic curve E, given a base level P on the curve and an integer okay. One other level Q on the curve is the results of multiplying P and okay utilizing the curve’s level addition operation.
First, think about an enormous piece of paper, on which is printed a sequence of vertical and horizontal strains. Every line represents an integer, with the vertical strains forming x-class elements and horizontal strains forming the y-class elements. The intersection of a horizontal and vertical line provides a set of coordinates (x,y). Within the extremely simplified instance under, there may be an elliptic curve that’s outlined by the next equation:
y2 + y = x3 · x2
For the above equation, given a definable operator, it’s doable to find out any third level on the curve given any two different factors. This definable operator varieties a bunch of finite size. So as to add two factors on an elliptic curve, first perceive that any straight line that passes by this curve intersects it at exactly three factors.
If two of those factors are outlined as u and v, then draw a straight line by these factors to seek out one other intersecting level at w. Then, draw a vertical line by w to seek out the ultimate intersecting level at x. Now, u + v = x. This rule works for outlining one other imaginary level, the origin, or O, which exists at theoretically excessive factors on the curve. The issue seems to be fairly intractable, requiring a shorter key size — thus, enabling faster processing time — for equal safety ranges as in comparison with the integer factorization downside and DLP.
Mathematicians have studied the properties of elliptic curves for hundreds of years however solely started making use of them to the sector of cryptography with the event of widespread computerized encryption within the Nineteen Seventies. At this time, ECDLP is extensively thought of the mathematical basis for the safety of elliptic curve cryptography.
Components of recent cryptology
At this time, researchers use cryptology as the idea for encryption in cybersecurity merchandise and techniques that shield information and communications. A number of the key components of cryptology are the next.
Symmetric key cryptography
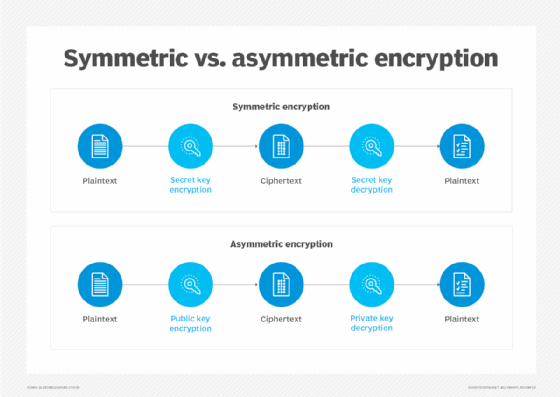
Symmetric key cryptography, generally known as secret key cryptography, makes use of the identical key to encrypt and decrypt information. Encryption and decryption are inverse operations, which means the identical key can be utilized for each steps, i.e., to scramble information to make it unreadable and in addition to unscramble it and make it readable. Symmetric key cryptography’s commonest kind is a shared secret system, wherein two events have a shared piece of knowledge, comparable to a password or passphrase, that they use as a key to encrypt and decrypt info to ship to one another.
Public key cryptography
Public key cryptography, also called uneven cryptography, is a cryptographic method that includes two separate keys: one personal and one public. Whereas each keys are mathematically associated to 1 one other, they serve totally different functions. The general public key, which isn’t secret, is utilized by the sender to encrypt the message. The one one who can decrypt the message is the individual holding the key personal key, i.e., the licensed recipient. For the reason that personal key’s wanted to decrypt the message that was initially encrypted with the general public key, public key cryptography gives a safe methodology for communication.
One well-known utility of public key cryptography is for digital signatures, which allow customers to show the authenticity of digital messages and paperwork and make it doable to ascertain safe communications even over insecure channels.
Cryptanalysis
Cryptanalysis is the observe of analyzing cryptographic techniques with the intention to discover flaws and vulnerabilities in them after which use these findings to strengthen the techniques. Basically, cryptanalysis is like penetration testing for cryptographic techniques.
For instance, cryptanalysts try to decrypt ciphertext with out information of the encryption key or algorithm used for encryption. They then use their analysis outcomes to assist to enhance and strengthen or substitute flawed algorithms.
Risk actors additionally use cryptanalysis strategies to interrupt ciphers or cryptographically secured communications. They could use varied strategies to do that, together with the next:
- Recognized-plaintext evaluation, the place some recognized plaintext-ciphertext pairs are mapped to seek out the encryption key.
- Chosen-plaintext evaluation, the place the encryption key’s decided by acquiring the ciphertext for some random plaintext.
- Man-in-the-middle assaults, the place they attempt to intercept the important thing by eavesdropping on the speaking events.
Cryptographic primitives
A cryptographic primitive is a fundamental cryptographic method, comparable to a cipher or hash perform, used to assemble subsequent cryptographic protocols. Many cryptographic protocols start through the use of some fundamental cryptographic primitives to assemble a cryptographic system that’s extra environment friendly and safer and gives stronger information authentication, confidentiality or integrity.
Cryptosystems
Cryptosystems are techniques used to encode and decode delicate info, comparable to private or monetary information, despatched over insecure networks. They incorporate separate algorithms for key era, encryption and decryption with the intention to hold information safe. The fundamental precept of a cryptosystem is the usage of ciphertext to remodel information held in plaintext into an encrypted message.
How is cryptology utilized in actual life?
One of the vital well-known functions of cryptology, particularly cryptography, is information safety. Cryptographic algorithms present the means to encrypt delicate information and to keep up its integrity and secrecy. These algorithms are often used to encrypt particular person recordsdata and even bigger storage volumes to safeguard the data contained in them from unauthorized entry and doubtlessly malicious interception.
Some frequent use instances of cryptology for information safety and/or for sustaining secrecy are the next:
- Digital banking.
- Different monetary transactions, e.g., ATMs and good bank cards.
- E-commerce.
- Medical databases.
- Authorized databases.
- Diplomatic communications.
- Navy communications.
Cryptography can be used to create digital signatures that assist to confirm the authenticity of knowledge despatched and obtained over a digital communication community. As soon as a doc is digitally signed, its recipients can use the sender’s public key to confirm that the sender is who they’re — their authenticity — and in addition to verify that the data in that doc was not illegally modified throughout its transmission. Digital signatures additionally facilitate nonrepudiation, which means a sender can’t deny the validity of a despatched message or deny that they despatched it. That is a crucial idea for verifying and guaranteeing lawfully binding documentation, e.g., contracts.
One other vital utility of cryptology is in nationwide safety. Quite a few governments use cryptology to intercept and research digital alerts, also called alerts intelligence. By monitoring international digital site visitors, authorities businesses are in a position to achieve insights into the capabilities, actions and intentions of international nations, together with their adversaries. This info guides their efforts to make sure the confidentiality, availability, integrity, authentication and nonrepudiation of the telecommunications and data techniques very important to nationwide safety.
Additional discover the variations between symmetric vs. uneven encryption, together with how they work and customary algorithms, in addition to their pluses and minuses.